75. Find Peak Element

发表于 更新于 阅读次数：

查找无续数组的峰值

LintCode链接

题目说明

给出一个整数数组(size为n)，其具有以下特点：

  • 相邻位置的数字是不同的
  • A[0] < A[1] 并且 A[n - 2] > A[n - 1]

假定P是峰值的位置则满足A[P] > A[P-1]且A[P] > A[P+1]，返回数组中任意一个峰值的位置。

样例

给出数组[1, 2, 1, 3, 4, 5, 7, 6]返回1, 即数值 2 所在位置, 或者6, 即数值 7 所在位置.

思路

  1. 一开始拿到题目觉得很简单，一个循环就好，1分钟写完代码 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    class Solution {
    public:
        /*
         * @param A: An integers array.
         * @return: return any of peek positions.
         */
        int findPeak(vector<int>& A) {
        	// write your code here
            unsigned length = A.size()-1;
            for (unsigned i = 1; i < length; ++i)
            {
            	if (A[i] > A[i-1] && A[i] > A[i+1])
            	{
            		return i;
            	}
            }
            
            return -1;
        }
    };
    提交之后，返回了一个红色的Time Limit Exceeded - -
  2. 经过仔细思考，可以按照二分法来做，这样时间复杂度可以降为O(logN)，具体思路，这里盗用下别人的图：

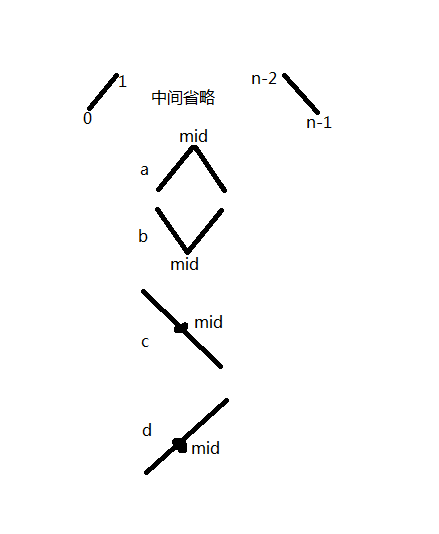
    中间值mid只会存在图中的四种情况：
    • 处于峰值，这时候就是我们要找的位置，直接返回就好
    • 处于最低点，则根据A[1] > A[0]判断，mid前面必有峰值
    • 处于下坡，则根据A[1] > A[0]判断，mid前面必有峰值
    • 处于上坡，则根据A[n-2] > A[n-1]判断，mid后面必有峰值
  3. 思路理清楚之后代码就很好解决了 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    class Solution {
    public:
        /*
         * @param A: An integers array.
         * @return: return any of peek positions.
         */
        int findPeak(vector<int>& A) {
            // write your code here
            unsigned left = 0, right = A.size() - 1;
            
            while (left <= right)
            {
                unsigned mid = (left + right) / 2;
                if (A[mid-1] < A[mid])
                {
                    if (A[mid] < A[mid+1])
                    {
                    	// 上坡;
                    	left = mid;
                    }
                    else
                    {
                    	// 最高点;
                    	return mid;
                    }
                }
                else
                {
                    right = mid;
                }
            }
            
            return -1;
        }
    };

总结

需要学会把复杂的问题进行拆分成各个小问题，然后一个个去解决。